Music, the Fibonacci Series and the Golden Mean

This essay was written by composer David Bruce, founder of 8notes.com for the following YouTube video. Subscribe to David's channel here

to follow new video essays on a wide range of musical topics.


I'm going to talk about Music, Fibonacci, and the Golden Mean, but first I want to talk about rabbits. Here's a little puzzle for you, first proposed by Leonardo Bonacci in his 1202 book Liber Abaci - the Book of the Abacus.



Bonacci's puzzle goes like this. If you put a pair of rabbits in a field, and they gave birth to a new pair of rabbits ever month, and it took each new pair a month to reach adulthood, how many rabbits would you end up with after a year?

counting month by month you get the following sequence, starting with one pair of rabbits

1

After a month they produce a pair of baby rabbits, so you've got two pairs

1 . . . 2

At the end of the second month the orginal pair produce two more babies, so you end up with three pairs in total

1 . . . 2 . . . 3

After three months the original rabbit couple produce another new pair of babies, while the oldest baby rabbits have reached adulthood and given birth to their own first babies, giving five pairs

1 2 3 5

After four months you've got three adult pairs and two baby pairs

1 2 3 5

After five months you've got five adult pairs and three baby pairs

1 2 3 5 8

After six months, 8 adult pairs and 5 baby pairs

1 2 3 5 8 13

and so on, like this

1 2 3 5 8 13 21 34 55 89 144 233 ...





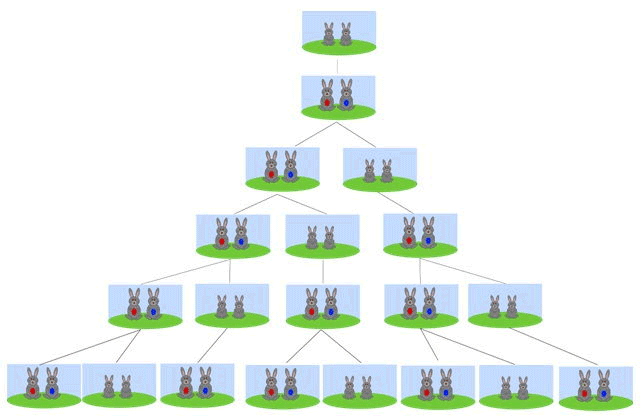
So, the answer at the end of one year is.... a lot of rabbits.

Now, maybe this number sequence looks familiar. What Leonardo Bonacci, better known by his nickname, Fibonacci, had uncovered with the help of his rabbits is the so-called Fibonacci Sequence.



You'll notice that each new term in the sequence is produced by adding together the two previous terms,

1 2
1 + 2 = 3
1 2 3
2 + 3 = 5
1 2 3 5
3 + 5 = 8
1 2 3 5 8
5 + 8 = 13
1 2 3 5 8 13


and so on, giving the famous sequence of Fibonacci Numbers

And it's not just rabbits, these number seem to appear everywhere in nature, in the number of petals on a plant, in the whirl of a pine cone ,in the growth of seashells and even in the flight paths of birds of prey. It's amazing to think that some of the most beautiful aspects of nature come through the application of the mathematics of the Fibonacci Series.

So this connection between mathematics and beauty has led musicologists to question whether music - that most mathematical of arts - could also have some Fibonacci numbers hidden within in.

Now there are all sorts of quite dubious theories you can find online about this, about how there are 13 chromatic notes in the octave, 8 white notes, and 5 black notes, or how various fibonacci ratios do generate musical intervals we recognise; but for me the most interesting area is how the proportions of the series might have affected - whether consciously or unconsciously, the way a piece of music is composed and structured.

There's a great example that's short enough to include in its entirety - it's the first of Chopin's preludes op.28 in C major. The piece is 34 bars long, with a climax at bar 21, the first major chromatic event in bar 13 and the opening statement lasts 8 bars, so 8, 13, 21, 34.

A perfect Fibonacci sequence.

Have a listen and judge for yourself whether these constitute audible events.

Chopin - Prelude in C Op.28 No.1

Another plausible example is the first movement of Mozart's Sonata in C Major, K. 279 which has 100 measures, whose main sections come at bar 62 and 38, very close to fibonnaci proportions

Now no one is suggesting that Chopin consciously worked with Fibonacci numbers, which weren't widely known about until the 1870s, but I think the most convincing aspect in the Chopin is the placement of the climax of the piece, which happens at this place known as the Golden Section, also known as the Golden Ratio or Golden Mean.

The Golden section- is the division that cuts a fixed length in such a way that the shorter portion bears the same ratio to the longer portion as the longer portion bears to the whole length.

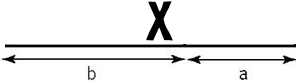
The actual ratio is about 1.618 often written as the Greek letter Phi.



Phi is intimately connected to Fibonacci, and you can see this in the maths, if you look at the ratios between successive numbers in the Fibonacci Sequence, the higher up you go, the closer and closer they get to this Golden Ratio.
2:3 = 1.5
3:5 = 1.66666666
8:5 = 1.6
13:8 = 1.625
21:13 = 1.6153846
34:21 = 1.6190476
55:34 = 1.617647


Unlike the fibonnaci series, The Golden Ratio has been known and studied since Ancient Greek times. It represents a point on a line that is neither a third nor a half, and some argue that when a work of art or a building incorporates the ratio, it will look better, look more 'in proportion'. Leonardo da Vinci certain knew about it, illustrating a book called "De Divina Proportione" (The Divine Proportion) by Luca Pacioli.



published in 1509. And there's some evidence some of his paintings are structured around the Golden Section although this is all hotly debated.

In architecture, the Great Mosque of Kairouan in Tunisia built in 670AD seems to have a consistent use of Golden Section proportions throughout.



Finding such comparable examples in the structure of music is more challenging, at least before the 20th Century. And of course there's the major problem that music operates in time, so you can only tell that you're at a golden section of a piece in retrospect, once you've heard the whole length of the piece. But it's certainly interesting to consider how quite a lot of pieces do seem to have a major climax around this point in their structure.

Fibonacci's work really came to wider public knowledge from the mid 1870s onwards, when French mathematician Eduoard Lucas named and studied them,



and from where they filtered into the minds of French symbolist artists, and then on into the work of composers like Debussy and Ravel. Which is why we start seeing a sudden plethora of Fibonacci-style structures in pieces from this time onwards.

Musicoligists like Roy Howat and Erno Lendvai have analysed pieces by Debussy, Ravel and Bartok





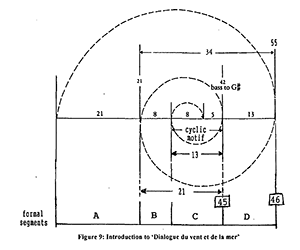
and found evidence that they are structured using Fibonacci sequences. Howat claims for example that the formal boundaries of Debussy's La Mer, correspond exactly to the Golden Section. And Howat delves deep into the piece uncovering fibonacci numbers and golden sections wherever he goes. For example, the 55-bar long introduction to Dialogue du vent et la mer can be broken down into 5 sections of 21, 8, 8, 5, and 13 bars in length, and the golden mean point of bar 34 is marked by the introduction of the trombones.



It's not really known though how much these composers knew of these ideas or applied them to their work. Perhaps the most suggestive piece of evidence that Debussy really did have mysterious mathematical considerations in mind when composing at least some of his pieces comes in an enigmatic letter to his publisher Jacques Durand written in 1903 about the corrected proofs of his piano piece "Jardins sous la pluie" in which he writes

"You'll see... that there's a bar missing -- my mistake . . . as it's not in the manuscript. However, it's necessary, as regards number; the divine number."

From Debussy's time onwards, composers increasingly started consciously composing pieces using Golden Section and fibonacci numbers. Krenek, Nono and Stockhausen are all known to have used them. Whether they are anything more than a curiosity, I'm not totally convinced. Too often these studies seem to rely on picking out pretty arbitrary points to justify the measurement of a particular number. But despite that, it's hard to escape the feeling that there must be some kind of connection between these numbers and music. No one can deny these number exist, and that they occupy a central place in our experience of beauty in the natural world.